在这篇文章里,我想要介绍一下代数几何里一个很经典的定理——贝祖定理 (Bézout’s theorem) 和它的一个有趣的推论——帕斯卡定理 (Pascal’s theorem)。让我们一起来欣赏一下抽象的力量——这是一个不需要画图也可以证明平面几何定理的过程!
帕斯卡定理
帕斯卡定理,是指圆锥曲线的内接六边形其三条对边的交点共线。在圆锥曲线是圆的时候,如下面这个(丑到爆炸的)图所示
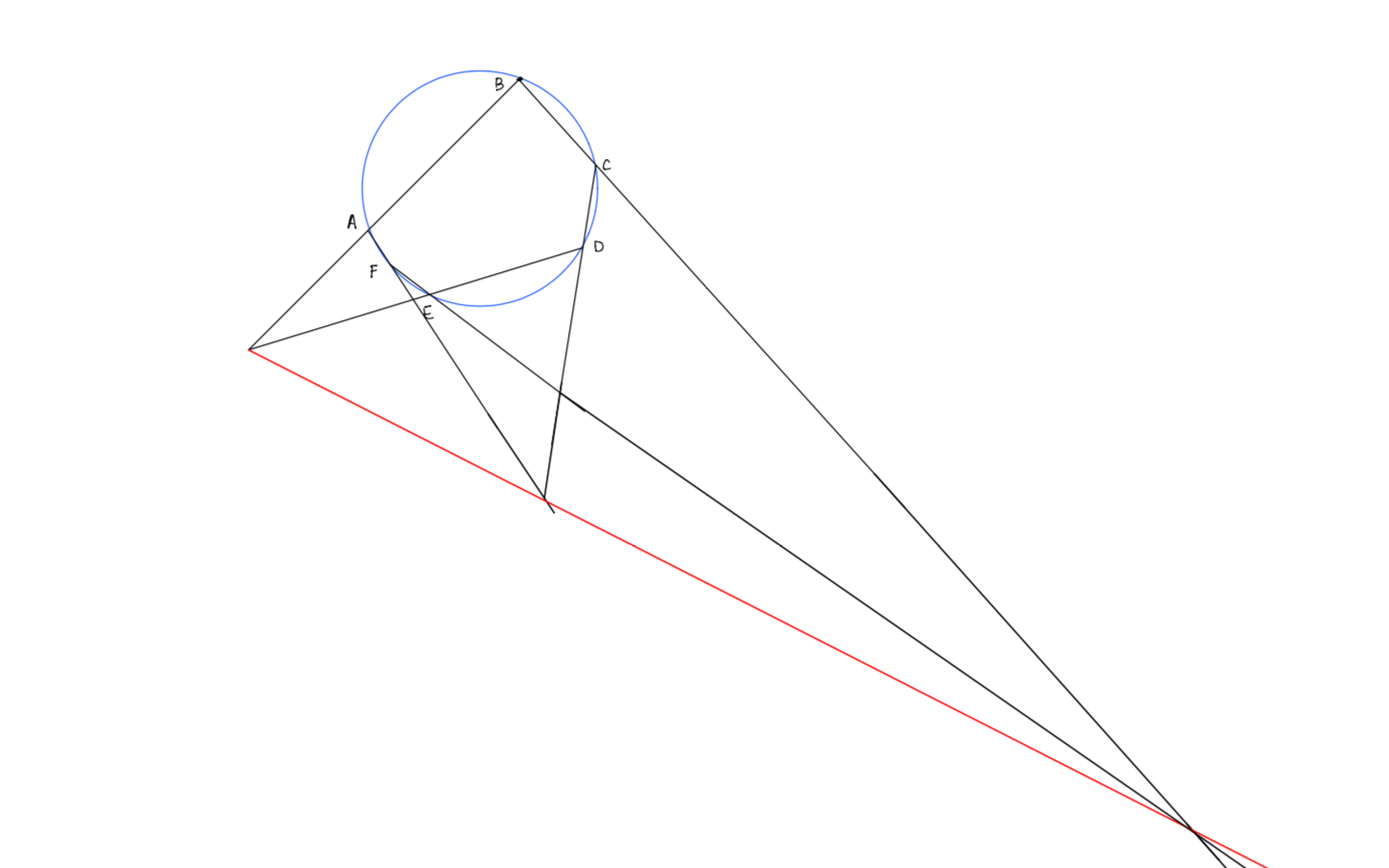
这个定理有很多证明,比如我们可以用梅涅劳斯定理来证明圆的情形,参见帕斯卡定理 。搞竞赛的小伙伴说不定还自己证明过。对于的任意圆锥曲线,它们可以投影变换成圆,所以这个命题对任意圆锥曲线都成立。
当这个圆锥曲线退化成两条相交直线的时候,帕斯卡定理就退化成了帕普斯(六边形)定理 (Pappus’s hexagon theorem)。
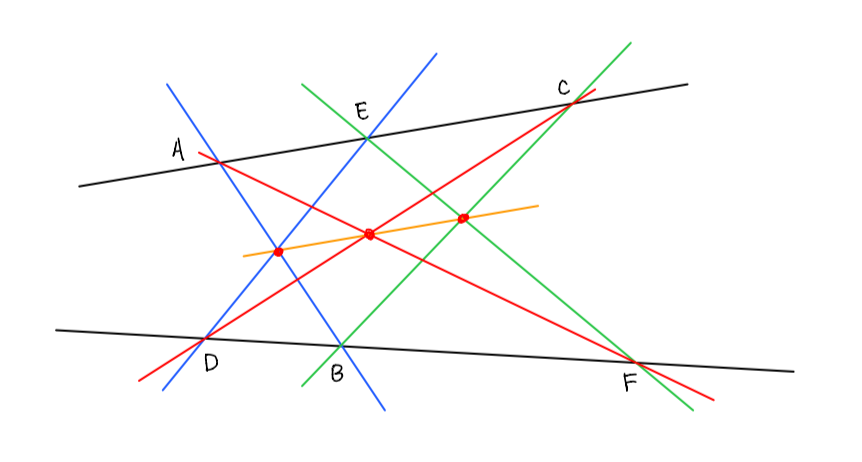
这个定理也是有各种经典的证明。单单算我在博士期间上过的组合课,就看到好几种不同的证明了。最近学到的一种是用 Grassmann-Cayley 代数证的(这也是一个不错的 topic,以后可以聊聊)。上图也是我那门课我自己记的笔记的截图。
而这篇文章主要想要探讨的,不是用这些“硬算”的办法来证明这(两)个定理。我即将介绍的,是一种抽象的数学技术证明的方法。我们将再一次见证数学的抽象的力量!
代数几何
大家可能多多少少听说过代数几何是如今数学研究的热门学科。但是代数几何到底是个啥?和我们上的那门叫“代数与几何”的课又有什么区别?
笼统的说,代数几何就是研究多项式的零点。一个多项式的所有零点构成的集合,称为一个代数簇 (algebraic variety)。一个简单的例子就是任意一个数轴 $\mathbb{R}$ 上的点,都是一个代数簇——比如 $x=1$ 就是 $x-1=0$ 的零点。同样的,任意有限多个点也是代数簇,比如我们有 5 个点 $0,1,2,3,4$,那这个集合是 $x(x-1)(x-2)(x-3)(x-4)$ 这个多项式的零点。我们上面提到的圆,也是一个代数簇。回忆一下,单位圆在二维平面 $\mathbb{R}^2$ 上对应的方程是 $x^2+y^2=1$。所以单位圆就是多项式 $x^2+y^2-1$ 的零点。当然二维平面上任意一条直线也是一个代数簇。特别的,类比一维的有限个点的情形,我们知道任意有限个直线的并集也是代数簇!它是这些直线对应的多项式的乘积多项式的零点。当然,这个操作看起来很无聊,就是把有限的一些东西摆在一起(取并集)。确实,它和前面一条线、一个圆有着本质的区别。数学家们管这种区别叫(不)可约性 (irreducibility)。简单的说,一条线、一个圆这样的,看起来就是一整块,没法分解成(有限的)更小的代数簇的东西,叫做*不可约 (irreducible)代数簇。而后面那个把一堆不可约代数簇并起来的,就是可约 (reducible)*代数簇。
还有一个很重要的特点,就是代数簇的次数 (degree)。粗略的说,既然一的代数簇是一个多项式的零点,那么这个多项式一定是某些次数的多项式,我们定义这个代数簇的次数就是这个多项式的次数。次数为什么重要呢?比如一维的情形,多项式的次数基本就决定了你的代数簇的点数。这里有一个小问题,那就是有重根怎么办?比如 $(x-1)^2$ 是一个二次多项式,但是它只有“一个”零点 $x=1$。这里我们就要发挥一下中文的“博大精深”:这里的次数不仅仅释作次数 (degree),可以释作重数 (multiplicity)。比如说上面这个例子里,虽然 $x=1$ 是唯一的一个零点,但是它却出现了两次!假如带上重数,那么这些多项式的次数就是点的个数。到了二维就不太一样了,随便一次还是二次甚至一百次的多项式,它们往往都有无穷多的点。但是我们还是有一些观察:比如二维情形下,一次多项式(对应的代数簇)只能是直线;你想要曲线,至少需要二次。
拼图的最后一块🧩,就是全空间的选取了。注意到 $x-1$ 在一维空间 $\mathbb{R}$ 中是一个点;但是同一个多项式 $x-1$ 放到二维空间 $\mathbb{R}^2$ 中看,就是一条线了!所以我们到底在哪个空间里考虑这些多项式,是很重要的事情。事实上,我们既不在 $\mathbb{R}$ 也不在 $\mathbb{R}^2$ 中考虑!不在 $\mathbb{R}$ 中考虑好理解,因为我们最终要证明一个平面几何的定理,一维的平面几何——有兴趣的读者可以自己研究😂。那为什么也不在 $\mathbb{R}^2$ 中呢?可能有些人知道一个名词,叫做“射影空间”。它的想法很简单:我们知道二维欧氏空间中,任何两条直线要么平行要么香蕉🍌,哦不,相交。但其实还可以换一个说法:“欧氏平面”里的任意两条直线总相交!那平行的怎么办?没关系,我们把他们相交的无穷远点补上就好了!所谓的射影空间 $\mathbb{P}^2$ 就是在 $\mathbb{R}^2$ 的基础上补上所有的无穷远点的集合。上面提到的帕斯卡定理、帕普斯定理,其实都是在射影空间中成立的定理。特别是帕普斯定理,它要求两条相交的直线,但其实两条平行直线也是可以的——它们在射影空间中相交于无穷远点!
贝祖定理
我们终于可以开始介绍(疯狂简化后的)贝祖定理了。
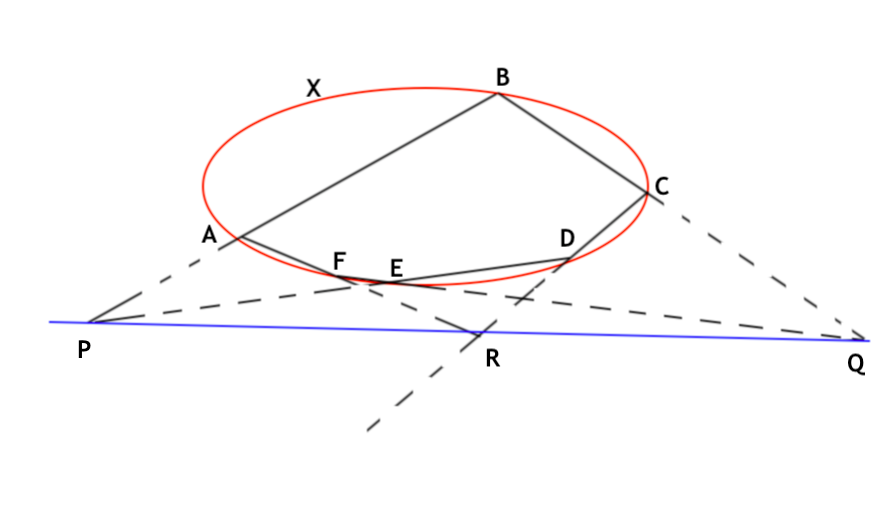
首先,这六条线没有哪条线包含了另一条线,所以我们可以应用贝祖定理(令 $X=X_1$ 和 $Y=X_2$),我们知道它们的交是一个次数为 $\deg(X_1)\cdot\deg(X_2)=3\times 3=9$ 的代数簇。刚刚我们说过没有两条直线互相包含,那么几条直线交出来的是什么?当然是点了!所以我们得到一个次数为 9 的一维代数簇。回忆我们之前讨论过,一维的情形下,次数 = 点的个数。所以 $X_1$ 和 $X_2$ 交于 9 个点!其实我们已经知道这 9 个点了——就是 $A,B,C,D,E,F,P,Q,R$ 。所以我们得到一个小结论:$f_1$ 和 $f_2$ 在这九个点上都等于 0。
下面我们考虑 $X$ 上的任意一个不是上面提到的 $A,B,C,D,E,F$ 这 6 个点的点 $S$。我们声称:存在一个点 $S\in X$ 和两个不全为 0 的数 $a,b$ 使得 $a\cdot f_1(S)+b\cdot f_2(S)= 0$。假如存在一个 $S$ 使得 $f_1(S)=f_2(S)=0$ 那我们取 $a=b=1$ 就可以了。反之则总有 $f_1(S)\neq 0$ 或者 $f_2(S)\neq 0$,那么取 $b=-f_1(S)$ 和 $a=f_2(S)$,则 $a\cdot f_1(S)+b\cdot f_2(S) = f_2(S)\cdot f_1(S)-f_1(S)\cdot f_2(S) = 0$。所以这样的数 $a,b$ 和点 $S$ 总存在。
下面令 $X’$ 是多项式 $af_1+bf_2$ 的零点集。我们知道 $A,B,C,D,E,F$ 都是 $f_1$ 和 $f_2$ 的零点,自然也是 $af_1+bf_2$ 的零点。所以 $X’\cap X=\{A,B,C,D,E,F,S\}$ 交于 7 个点!但是我们知道 $\deg(X’)=\deg(af_1+bf_2)=3$,所以 $\deg(X’\cap X)=\deg(X’)\cdot \deg(X) = 3\times 2=6$ ($X$ 是一个二次曲线)。所以这个结论违反了贝祖定理!完了,数学大厦崩塌了!【皮这一下很开心😂】
且慢,我们说这个结论违反贝祖定理,起码它得可以应用贝祖定理呀!结论不成立告诉我们,这里面一定有不满足贝祖定理的条件的地方。返回去看看贝祖定理的条件,哪里有可能不满足?自然是我们的额外假设:没有 $X$ 的某个不可约子集(比如 $X$ 中的一条线)完全包含在 $Y$ 中!所以 $X$ 一定有一个不可约的子集完全包含在 $X’$ 中。而我们已经知道 $A,B,C,D,E,F$ 这 6 个“墙头草”既在 $X$ 中也在 $X’$ 中。所以唯一可能就是 $X$ 整个都在 $X’$ 中!所以我们可以写成 $X’=X\cup L$, 其中 $L$ 是某个我们还不咋了解的代数簇。
根据我们的观察,假如一个代数簇分解成了两个代数簇的并,那么它的次数应该是这两个代数簇的次数的和(例如几条直线的并)。现在由于 $X’=X\cup L$ 而 $\deg(X’)=3,\deg(X)=2$,根据小学知识,我们知道 $\deg(L)=3-2=1$。我们前面聊过,次数为 1 的只能是直线!所以 $L$ 是一条直线。
最后,注意到 $P,Q,R$ 都是 $f_1$ 和 $f_2$ 的零点,所以它们都是 $af_1+bf_2$ 的零点,从而它们都在 $X’$ 中。我们又知道这三个点不在 $X$ 中,所以!它们只能在 $L$ 中!所以,换个说法,这三个点在同一条直线 $L$ 上!🎉🎉🎉 $\blacksquare$
后记
以上证明来自于 Andreas Gathmann 的代数几何讲义中的定理 6.2.5。我第一次学到它的时候真的被震惊了——从来没想到过抽象的代数几何可以给出如此经典且具体的平面几何的定理的漂亮的证明!从那儿以后就一直想着有一天想要写出来分享给大家,今天算是了却了一桩心愿。感谢你读到这里🙏。